Shape Matching in Javascript
When I was building stroke order quizzes in Hanzi writer one of the core challenges was determining if the shape of a stroke drawn by a user is similar to the correct stroke in the Chinese character. However, as I was working on Hanzi Writer I didn’t find much in the way of javascript modules to help with curve matching, so I extracted the logic from Hanzi writer and created a new library called curve matcher. We’ll go through the theory of curve matching and how you can do curve matching in Javascript below.
NOTE: If you want to skip to the chase and aren't interested in how this curve matching actually works you can take a look at the shapeSimilarity function in curve matcher. shapeSimilarity(curve1, curve2) implements everything we're going to talk about below, and outputs a number between 0 and 1 to describe how similar the curves are.
Fréchet Distance
Fréchet distance is a metric which can be used to determine how similar 2 curves are. You can visualize the concept behind Fréchet between curves by imagining a person walking their dog on a leash. The person walks along the path of one of the curves, and the dog walks along the path of the other curve. They each try to vary their speed as they walk to keep the leash as short as possible. The Fréchet distance between the curves, then, is how long the leash must be to allow the person and dog to walk each curve while staying connected.
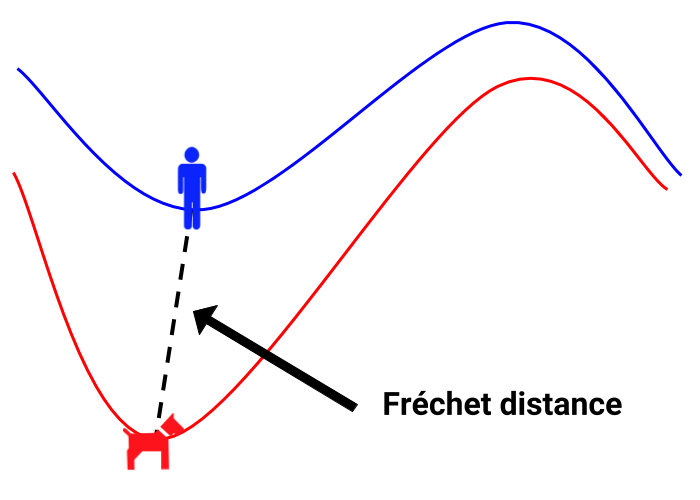
Calculating Fréchet Distance
You can estimate Fréchet distance between 2 curves using a simple discrete Fréchet algorithm. The algorithm is from the paper Computing Discrete Fréchet Distance. In javascript, you can use the curve matcher library to calculate this value for you:
import { frechetDistance } from 'curve-matcher';
const dist = frechetDistance(curve1, curve2);
In the above, the curves are in the form: [{x: 10, y: 15}, {x: 13, y: 12.3}, ...].
Improving Discrete Fréchet Accuracy
The discrete Fréchet distance algorithm above has a critical limitation, however, which is that it is only as accurate as the size of the line segments of the curves you pass in. So, you can increase the accuracy of the discrete Fréchet algorithm by subdividing the segments of the curve into smaller line segments. The smaller the line segments in each line, but the more accurate it will be.
For example, if our curve looks like the curve below:
[
{x: 10, y: 10},
{x: 20, y: 30},
{x: 30, y: 10},
]
We can increase accuracy by subdividing the curve further, for example:
[
{x: 10, y: 10},
{x: 15, y: 20},
{x: 20, y: 30},
{x: 25, y: 20},
{x: 30, y: 10},
]
Here, we added the point {x: 15, y: 20} between {x: 10, y: 10} and {x: 20, y: 30}. {x: 15, y: 20} is already on the line between {x: 10, y: 10} and {x: 20, y: 30}, so adding this point doesn’t change the shape of the curve at all, but it decreases the length of each line segment so our discrete Fréchet distance calculation will be more accurate.
The curve matcher library has a function called subdivideCurve which does exactly that. We can use this function to increase the accuracy of our Fréchet distance calculation by breaking up line segments to guarantee that no line segment is longer than, for instance, length 0.05:
import { frechetDistance, subdivideCurve } from 'curve-matcher';
const dividedCurve1 = subdivideCurve(curve1, { maxLen: 0.05 });
const dividedCurve2 = subdivideCurve(curve2, { maxLen: 0.05 });
// Now, this is guaranteed to give a result that's off by less than 0.05
// from the true frechet distance between these curves
const dist = frechetDistance(dividedCurve1, dividedCurve2);
We can make the maxLen smaller to increase accuracy of the discrete Fréchet distance calculation, but the calculation will take longer the more we subdivide the curve.
Normalizing Curves for Shape Matching
Unfortunately, Fréchet distance doesn’t only depend on the shape of the two curves. If the curves have different sizes or are far apart then the Fréchet distance between them maybe be large even if the curves have identical shapes! If that’s alright for your use-case, congrats, you’re done! Otherwise, if you only want to get a measure of how similar the shapes of the curves are then you’ll need to normalize the curves to account for translation, scaling, and rotation before determining discrete Fréchet distance. This can be done using Procrustes analysis. The name Procrustes comes from a villain in Greek mythology who used to force his victims to fit into his bed either by stretching their limbs of cutting them off. We won’t be doing anything nearly as violent here, but we’ll stretch and shrink our curves so that their location and size is as uniform as possible!
Before beginning with Procrustes analysis, we need to redistribute the points along our curves so they’re evenly spaced. For any given curve, you can add more points to some parts of the curve and less in others while still maintaining the same general shape of the curve. For example, the curves below are identical but have different distributions of points:
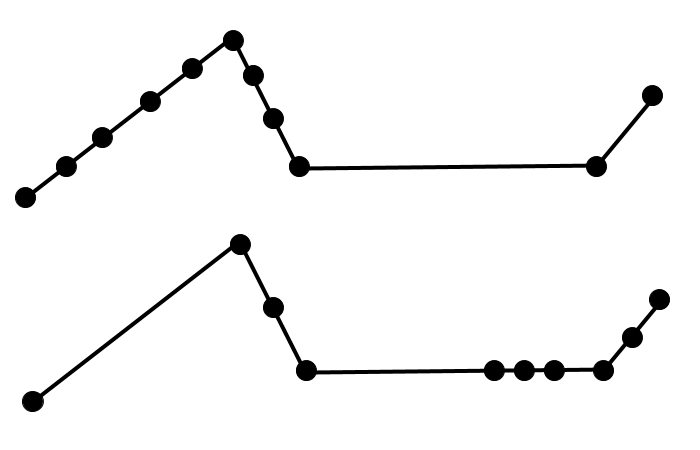
This is a problem because when we try to normalize the curves based on the mean and RMS of the points of the curve, the 2 curves above will be translated and scaled differently despite both being identically shaped!
Fortunately, we can use a function from curve matcher to redistribute the points in our curves so the points are equally distributed along the length of the curve. Below we use the function rebalanceCurve to redraw our curves so they both are made of 50 equally spaced points:
import { rebalanceCurve } from 'curve-matcher';
const balancedCurve1 = subdivideCurve(curve1, { numPoints: 50 });
const balancedCurve2 = subdivideCurve(curve2, { numPoints: 50 });
Now, we can use Procrustes analysis to try to make our 2 curves have the same location and size so that we can just compare the actual shape of the curves to each other. If you’re interested in the math involved in this you can read about it here. Otherwise, you can just use the procrustesNormalizeCurve function in curve matcher:
import { rebalanceCurve, procrustesNormalizeCurve } from 'curve-matcher';
const balancedCurve1 = subdivideCurve(curve1, { numPoints: 50 });
const balancedCurve2 = subdivideCurve(curve2, { numPoints: 50 });
const normalizedCurve1 = procrustesNormalizeCurve(balancedCurve1);
const normalizedCurve2 = procrustesNormalizeCurve(balancedCurve2);
Calculating shape similarity
Now that we have normalized curves we can go back to calculating Fréchet distance as a metric of how similar the shapes of these 2 curves are. With scale and translation normalized, the worse possible Fréchet distance we can get is the length of the longest curve. So, let’s use that fact to calculate similarity!
import {
curveLength,
frechetDistance,
procrustesNormalizeCurve,
rebalanceCurve,
} from 'curve-matcher';
const balancedCurve1 = subdivideCurve(curve1, { numPoints: 50 });
const balancedCurve2 = subdivideCurve(curve2, { numPoints: 50 });
const normalizedCurve1 = procrustesNormalizeCurve(balancedCurve1);
const normalizedCurve2 = procrustesNormalizeCurve(balancedCurve2);
const dist = frechetDistance(normalizedCurve1, normalizedCurve2);
curveLen1 = curveLength(normalizedCurve1),
curveLen2 = curveLength(normalizedCurve2),
const maxCurveLen = Math.max(curveLen1, curveLen2);
// similarity == 1 means the curves have identical shapes
const similarity = 1 - dist / maxCurveLen;
What about rotation?
We still haven’t corrected for the rotation between the 2 curves yet! There’s a Procrustes analysis technique for correcting rotation between 2 normalized curves implemented by the procrustesNormalizeRotation function in curve matcher, but in practice this only works well if curves have a pretty similar shape. An easy brute-force solution is to try several different rotations of the curves and see which rotation results in the smallest Fréchet distance. At this point though, you may as well just use the built-in shapeSimilarity function in curve matcher. shapeSimilarity will do everything we’ve discussed so far, as well as correct for rotation between the curves. Calculating similarity with this function is shown below:
import { shapeSimilarity } from 'curve-matcher';
// shapeSimilarity handle rebalancing the curves, normalizing them
// via procrustes analysis, correcting rotation, and calculating
// similarity via frechet distance
const similarity = shapeSimilarity(curve1, curve2);
And that’s just about it! Take a look at curve matcher and happy curve matching!